Geodatabase... GIS Database... Part 2

Precision and Integer bytes
In order to fully understand precision and spatial domain, you need understand the computer binary number system.
Bits - A digit in the binary number system is called a bit. The smallest binary digit is 0. The next, and only other, digit is a 1. Compare this with the decimal number system, which uses ten digits between 0 and 9, inclusive.
Bytes - In the decimal number system, when you run out of values for a given digit you need to use an additional digit to store a larger number. For example, if you wanted to store a number bigger than 9, you would need to add a second digit to produce the next largest number, 10. The binary number system works the same way. After exhausting both values for a single digit, you need to add an additional digit to store a larger number. For example, the smallest (positive) binary number is 0. The next largest is 1. After that, you need to add a second digit to represent the next highest number: 10. The next few numbers in this sequence are 11, 100, 101, 110, 111, and 1000. The decimal equivalents of these binary numbers are 3, 4, 5, 6, 7, and 8.
From this progression, it is easy to see that many binary digits are required to store relatively small numbers. Therefore, programmers usually work with groups of bits called bytes. A standard byte contains 8 bits.
The meanings of bits - Like decimal digits, binary digits indicate some quantity, such as the distance along one axis from the origin of a coordinate system. The decimal number 4 may represent a geographic location four meters away from the origin along the Y axis. Likewise, the number 40 could represent a location forty meters away from the origin. With only nine digits, you can construct larger numbers like 40 by assigning a certain weight to each digit. In this example, the digit “4” in “40” is weighed ten-times more than the digit “0”. So, 40 actually means (4 * 10) + (0 * 1). In another example 3,862 can be expressed as (3 * 1000) + (8 * 100) + (6 * 10)+ (2 * 1).
Binary numbers work in exactly the same way. The only difference is that each digit represents a successively higher power of two, rather than a higher power of ten, because the binary number system only has two digits instead of the ten available in the decimal system.
For example, the number 1101 can be expressed as (1 * 8) + (1 * 4) + (0 * 2) + (1 * 1) for a total of 13, in decimal notation.
Another convenient way to think about binary digits is that they express the presence or absence of a value. Continuing the 1101 example, you could say “yes, there is an eight; yes, there is a four; no, there is not a two; and yes, there is a one”. Computers are well-suited to processing these types of presence/absence indicators because the transistors etched into their CPUs may exist in two states: allowing electricity to flow through, or preventing electricity from flowing through. Correlating the presence or absence of an electrical current to the presence or absence of values represented by binary digits allows engineers and programmers to build sophisticated systems based on a simple concept.
Bits and geodatabase coordinates
Geodatabase stores coordinate values using a signed, positive, 32-bit integer data type. One of the 32 bits is used as a sign bit, indicating positive or negative, leaving 31 data bits for storing coordinate information. If all of these 31 bits are set to 0, the resulting decimal number is 0.
This is the smallest coordinate value geodatabase can store internally. If all of the bits are set to 1, the resulting decimal number is 2,147,483,647. This is the largest coordinate value geodatabase can store internally.
These two extremes define the fixed, finite size of the geodatabase spatial domain. The data types used to store and process coordinate values are necessarily hard-coded into the software and cannot be altered. Note, however, that these values are unit-less.

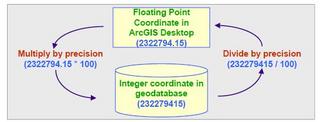
On a feature-class by feature-class basis you can set the 2,147,483,647 integer storage units to represent meters, miles, light-years, or any other unit of linear measurement by choosing the appropriate precision value. This gives you flexibility to stretch those roughly two-billion units over any sized geographic area.
So... now you can understand the secret of storing X/Y or Latitude/Longitude coordinates in GIS. This has been used for many years... and now its capabilities are not only limited to file storage but also enterprise storage like Oracle, SQL Server, DB2 etc.